Deutsche Seite
It works !?
This article describes a theoretical experiment,
which was published 1974 in the journal "Sience" by the
chemist Octave Levenspiel. The experiment, known as Levenspiel's
fountain ,
is discussed as
a perpetual
motion machine
of second kind.
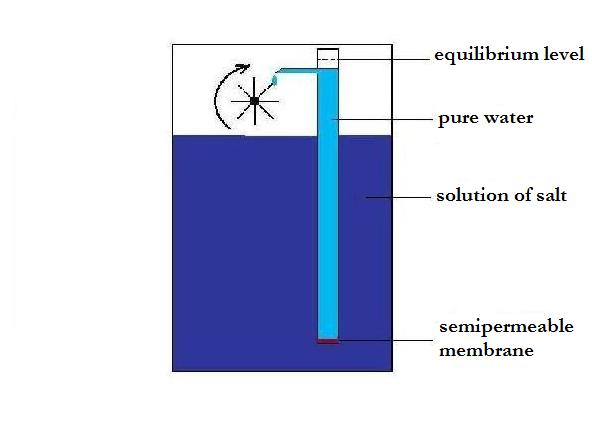
The here described
variation of
"Levenspiel's fountain" has a wheel , which is in constant
rotation by falling water
drops. In this device a tube with pure water immerse in a solution
of salt. The lower end of the tube is closed by a semipermeable
membrane.
If the tube is short, the water level inside would be lower than
outside, because of the osmotic pressure. But when the tube immerse
deeper
and deeper in the solution, this relation will change to a higher level
inside, because the density of the salt solution is higher and so the
hydrostatic pressure will grow faster. When the tube is long enough,
falling water drops result a continual motion of the wheel.
Exist in a closed sytem a rotating wheel, which
motion is not
limited by the formation of a final equilibrium, this is in
contradiction
to the second law of thermodynamics. It is a
perpetual motion machine of second kind.
The question here is, if it is possible-why ? The peculiarity, that the
tubes have to be very long, because the osmotic pressure is even with
low concentrations high, should be not important to a theoretical
discussion.
At first we imagine, that there is no dropping out by the
added side tube. In this case the water level would rise to
the equilibrium line. In this equilibrium state no further motion
is possible. The connection between the solution and pure water exist
only by the semipermeable membrane. Single water
molecules can move through the membrane in both directions and so it is
a reversible connection between the systems.
If we add the side tube, the connection there is
only in one direction, because a single water drop can only fall
down. The irreversible step prevent the
genesis
of a final equilibrium, which would stop the process.
So we can assume, that for a endless motion we need both processes,
reversible and irreversible.
An explanation for the importance of this priciple is available
in the link Irreversibility
against thermodynamics .
back
next
